第一作者：余亚雄、鲁峰

通讯作者：张晨曦

通讯单位：清华大学、鄂尔多斯实验室

文章链接：

https://doi.org/10.1016/j.ces.2023.119564

主要结论

近日，清华大学-鄂尔多斯实验室魏飞团队在气固流态化双分散颗粒非对称分布的指认与机制分析取得重要进展。这项研究耦合双光纤与信号偏转重构方法实现了双分散颗粒在气泡相与乳化相结构分布的精细测量，揭示了细颗粒在气泡相聚集的非对称分布现象。将流化床内的气泡视为“精馏塔板”建立了简明的通量模型定量描述这一选择性分离现象并为工业流化床内气固相结构调控提供指导。相关成果以“流态化中细颗粒的非对称分布”(Discovery of asymmetric distribution of fine particles in fluidization using signal deflection reconstruction measurement)为题发表于《化学工程科学》(Chemical Engineering Science) 期刊上，该期刊与AIChE Journal，Industrial & Engineering Chemistry Research并称为“化工三大刊”。

研究背景

颗粒流中的非对称分布指的是不同种类颗粒在展现出不同的运动特性，反映了颗粒的选择性分离行为。这种现象在多个领域都有观察到，比如巴西果效应、分仓颗粒布居分聚现象，以及双分散振动流化床内细颗粒更倾向进入颗粒速度脉动强的区域等。John R. Grace教授于1990年通过实验首次推测，在双分散气固流化床中，细颗粒相较于粗颗粒更倾向进入气泡，形成了非对称分布现象。然而，目前的实验测量技术，包括光纤探针、电容层析成像（ECT）、快速X射线层析成像和激光光度技术等，都难以实现对双分散颗粒的指认或准确测量双分散组分的固体体积分数，因此流化床内这一非对称分布现象尚没有得到实验验证。

为了解决这个问题，我们基于光纤探针的标定曲线对颗粒颜色敏感的特性，开发了一套信号偏转重构技术。该方法可以实现对颗粒的指认，并准确获取组分固含率，进而验证双分散流化床中存在的非对称分布现象。

图文导读

1.双分散流化床固体体积分数的测量——信号偏转重构技术

双分散系统有粗颗粒和细颗粒固含率这两个未知量，光纤探针仅能给出一个光纤信号作为约束条件，因此无法求解两个组分的固含率，也无法获得总固含率。如图1（a）所示，本文利用光纤标定曲线受颗粒颜色影响这一特点，通过染色对颗粒的光纤标定曲线进行偏转，得到另一个光纤信号作为约束条件。通过这两个约束条件可联立得到两组分的固含率。具体而言，我们在相同工况下开展两组实验：EXP-A和EXP-B。其中，EXP-A采用未染色的颗粒，EXP-B则采用染色的颗粒。由于少量的染色剂对颗粒的物性影响不大，因此可以认为EXP-A和EXP-B得到的统计结果完全一致。最后，通过信号偏转重构算法（公式（1））可以得到组分颗粒浓度或细颗粒的体积占比。为了验证该方法的准确性，我们采用已知组分占比的固定床对该方法进行了验证，如图1（b）所示，结果显示该技术能够准确得到颗粒的组分占比。

               

           

                                 

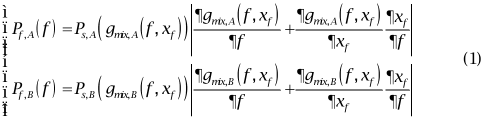
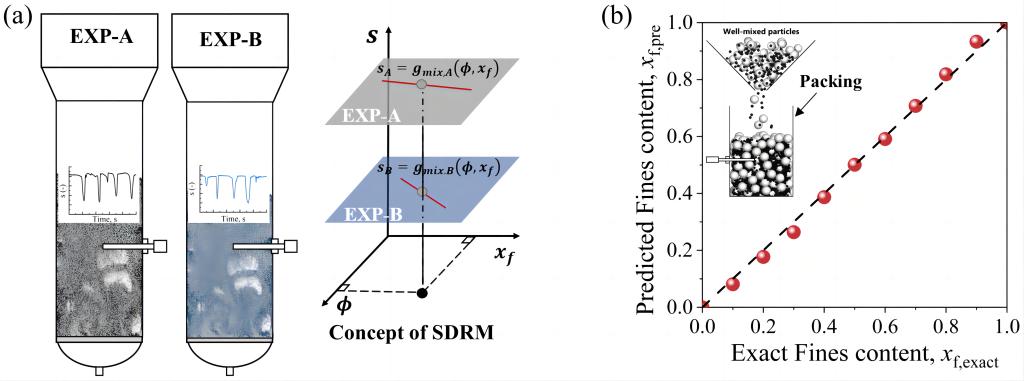
图1（a）信号偏转重构技术示意图；（b）基于固定床对信号偏转重构技术进行验证

2.流化床内的非对称分布现象

双分散流化床实验采用的是186 μm的粗石英玻璃珠和60 μm直径的细石英玻璃珠，对应的最小流化速度分别为3 cm/s和0.58 cm/s。入口流化气速约为粗颗粒最小流化速度的1.7倍。在流动达到稳定后，我们开始记录光纤信号强度。图2(a)展示了EXP-A和EXP-B的光纤信号随时间变化的情况。明显可以看出，染色前后信号强度存在显著差异，这种差异来源于光纤标定曲线的变化。随后，通过对数据的统计，我们得到了信号强度的概率密度分布，如图(b)所示。最后，应用光纤标定曲线和信号偏转重构算法，我们得到了总固含率的概率密度分布，结果展示在图(c)中。观察该图可发现，在高固含率的密相区域，粗颗粒和细颗粒对总固含率的贡献非常接近；而在总固含率较低的气泡区域，细颗粒对总固含率的贡献明显大于粗颗粒，说明气泡内细颗粒的体积占比大于密相区域；而且通过图（d）可以发现细颗粒的体积占比随着总固含率的增加呈现减小的趋势。以上实验结果说明，细颗粒相较于粗颗粒更倾向进入气泡区域。

                                 

图2（a）光纤信号强度随时间的变化；（b）光纤信号强度的概率密度分布；（c）固含率的概率密度分布函数；（d）细颗粒体积比随总固含率的变化。

3.非对称分布的通量模型

将气固系统分为两个部分，即高固含率的密相和低固含率的气泡相，二者之间形成的气泡界面即为相界面，如图3(a)所示。我们将相界面视为“精馏塔板”来描述这一非对称分布现象，假设颗粒通过相界面的过程是可逆的，并认为双分散颗粒之间没有相互作用。我们发现这种非对称分布是由于不同粒径颗粒在维持相分离方面的能力差异所致。具体来说，细颗粒的速度脉动强度更大，更难维持气泡和密相的相分离。在图3(b)中，我们展示了细颗粒的非对称分布，即细颗粒在气泡相与密相的体积占比之间的关系。该图显示，气泡内细颗粒体积占比更高，说明细颗粒相较于粗颗粒更倾向于进入气泡相；同时，通量模型能够准确预测这一现象，证明了该模型的有效性。

                                 

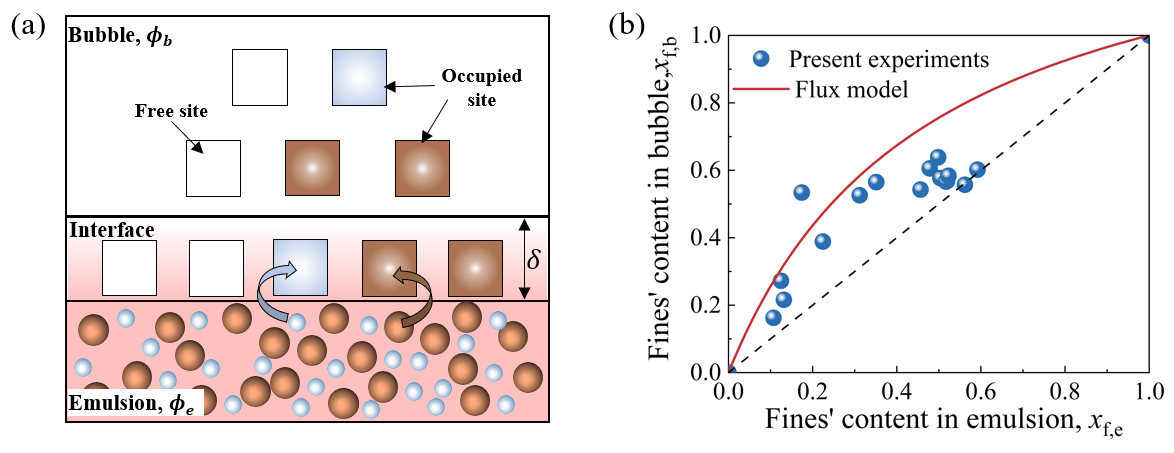
图3 (a) 双分散颗粒选择性分离示意图；（b）细颗粒的非对称分布

作者简介

余亚雄：博士，清华大学化工系魏飞团队助理研究员/博士后，于2022年获西安交通大学工学博士学位。主要从事颗粒流可压缩性实验和理论研究、CFD-DEM粗粒化模型及气-固介尺度本构关系构建。在Journal of Fluid Mechanics、AIChE Journal、Chemical Engineering Journal、Chemical Engineering Science及Industrial Engineering Chemistry Research等流体化工学术期刊累计发表文章十余篇，获2024年国家自然科学基金青年科学基金项目。

鲁峰：博士，清华大学魏飞团队助理研究员，主要从事高压流化床设计、多相流理论、新型大型储能技术、复杂矿物处理和功能材料制备等方面的研究。以第一作者在AICHE Journal(letter), Chemical Engineering Science, Physics of Fluids, International Journal of Hydrogen Energy等国内外学术刊物及会议期刊发表论文十余篇；申请专利9项，获2023年国家自然科学基金青年科学基金项目。目前为清华大学化工系在站博士后，从事流化床反应器设计，二氧化碳绿色转化，新型大型储能技术开发，电池材料制备工艺等相关课题项目研究工作